Visualsky Blog

Magnitudine superficiale al telescopio

È opinione comune che un telescopio fornisca immagini più "luminose". Un telescopio raccoglie più luce e quindi è naturale che le immagini siano più brillanti, giusto?
Se per "brillanti" si intende di intensità superficiale maggiore, sorprendentemente questo è sbagliato.Nel caso di un oggetto esteso, infatti, per valutare l'intensità superficiale che appare all'oculare di un telescopio occorre considerare due fatti: a) che il telescopio raccoglie più luce rispetto all'occhio, b) che questa luce è però distribuita su una immagine ingrandita.

In campo astronomico l'intensità luminosa superficiale si misura in magnitudini per secondo d'arco quadrato. Per esempio dire che una superfice ha intensità 17 magnitudini per secondo d'arco quadrato, significa dire che è come se su ogni quadratino di un secondo per un secondo d'arco ci fosse una stellina di magnitudine 17, che vediamo tutte assieme non risolte come un'area lattiginosa (Surface Brightness). Ad esempio un cielo molto buio e incontaminato non è nero, ma brilla di magnitudine superficiale 21.9 circa (The Brightness of the Night Sky).

Dunque, come appare un oggetto di intensità superficiale m quando è visto in un telescopio di diametro D ad un ingrandimento M?
I calcoli sono presto fatti:
a) rispetto all'occhio il telescopio raccoglie più luce in proporzione al rapporto fra le aree. Nella formula che segue G rappresenta il guadagno di luce tenuto conto delle perdite dovute a al sistema ottico (k è la trasmissione complessiva di luce, sempre inferiore a 1; vedi nota in fondo per una stima delle perdite). D e d sono rispettivamente il diametro del telescopio e il diametro della pupilla dell'occhio.

Per esempio un telescopio riflettore di 600 mm di diametro, rispetto a un occhio con pupilla di 6 mm raccoglie 10000 volte più luce (a prescindere dalle perdite k).
b) l'immagine ingrandita occupa un'area apparente che rispetto all'area reale è estesa proporzionalmente al quadrato dell'ingrandimento M. Per esempio la superficie della luna, che è di 0,2 gradi quadrati, a 100x occupa un'area apparente 10000 volte maggiore (il quadrato dell'ingrandimento) e quindi 2000 gradi quadrati.

Mettendo assieme i due fatti, si conclude che l'intensità superficiale al telescopio appare variata secondo il rapporto fra la (maggiore) luce raccolta e la (maggiore) area su cui è distribuita:

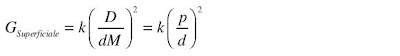
Possiamo pensare a G Superficiale come al fattore che rappresenta il guadagno di intensità superficiale del telescopio (analogo a G che è il guadgno di luce raccolta). Notare che nella formula il rapporto D/M è la pupilla di uscita del telescopio all'ingrandimento in uso. La formula è valida finantochè la pupilla di uscita p è minore del diametro d dell'iride dell'occchio. Se è maggiore (perchè si usa un ingradimento troppo basso per il diametro del telescopio) la formula non vale perchè non tutta la luce raccolta del telescopio entra nell'occchio. In questo caso si sta sfruttando solo una parte del diametro del telescopio che corrisponde alla sezione che entra nella upilla dell'occhio e che vale dM. Quindi se D è maggiore di dM è come se si avesse un telescopio diaframmato al diametro D'=dM
Non è difficile rendersi conto che per aumentare il guadagno superficiale occorre aumentare il diametro a pari ingrandimento. In questo modo aumenta il numeratore dell'espressione dentro le tonde nella formula. Il massimo diametro utilizzabile per un certo ingrandimento è però quello che produce una pupilla p pari al diametro d dell'iride e che per quanto detto vale dM. In questo caso il guadagno superficiale è quindi al massimo pari alla trasmissione complessiva di luce, che è sempre e comunque minore di uno. In altre parole l'intensità superficiale al telescopio è sempre inferiore a quella originale dell'oggetto.

Tenuto conto che i guadagni sono espressi in scala lineare, mentre in ambito astronomico le scale di intensità superficiale sono in magnitudini (che è una scala logaritmica), la formula per la magnitudine superficiale apparente al telescopio è la seguente:

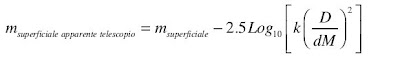
con l'avvertenza che il diametro D utilizzabile è al massimo uguale al prodotto del diametro dell'iride per l'ingrandimento dM.

Facciamo alcuni esempi (d=6mm, k=0.72):
- regione del trapezio di M42 di intensità superficiale 14.5; regione adiacente al trapezio di intensità superficiale <17 (Surface Brightness of Deep-Sky Objects Measured with a Digital Camera).
a) telescopio di 400 mm a 100x. Il guadagno di luce è 3200. L'area è ingrandita in superficie 10000 volte. L'intensità superficiale apparente è ridotta secondo il fattore 0.32. La magnitudine superficiale dell'immagine del trapezio al telescopio è 15.7. L'area adiacente è < 18.2.
b) telescopio da 800 mm a 100x. In questo caso la pupilla di uscita di 8 mm non è sfruttabile. Il diametro sfruttabile è 600 mm a 100x (che sono quelli la cui luce entra tutta nell'occchio supposto di diametro 6 mm). Il guadagno di luce, incluse le perdite, è 7200. L'area apparente è sempre 10000 volte maggiore. L'intensità superficiale al telescopio è ridotta di 0.72 volte. La magnitudine superficiale è rispettivamente 14.85 e <17,35.
c) telescopio da 400 mm a 66.6x. Si ottiene lo stesso risultato di prima. La differenza rispetto al caso b è che l'immagine è più piccola (a 66,6x invece che 100x) ma ha la stessa intensità superficiale (che è comunque meno dell'intensità superficiale originale).
d) telescopio da 100 mm rifrattorte (k=0.86) a 100x. Guadagno di luce 239. Area apparente 10000 volte. magnitudine superficiale apparente: 18.55 e < 21.05.

Ma se l'intensità superficiale al telescopio è sempre minore di quella originale, come mai si vedono oggetti deboli al telescopio che a occhio nudo non si vedono? La risposta, sorprendentemente, è che l'intensità superficile apparente non è critica, perchè l'occhio arriva a 24 e oltre. Il fattore critico è una combinazione di contrasto e dimensioni apparenti: per ogni intensità superficiale dell'oggeto e per ogni contrasto con lo sfondo esiste una dimensione minima. L'immagine a occhio nudo è sì più brillante, ma troppo piccola da essere rilevata. Optimum Magnified Visual Angle

Nota: esempio di calcolo della trasmissione per un telescopio. Telescopio newton con ostruzione 20% lineare (4% in area), riflettanze 90% su primario e secondario, oculare con trasmissione del 92%. k= 0.96 x 0.90 x 0.90 x 0.92 = 0.72.

Vedre anche: Lowering the threshold

posted by Mauro Da Lio @ 11:41 AM